• 推荐系统实例
  • 外围架构
  • 推荐系统架构
  • 推荐引擎的架构
    • 生成用户特征向量
    • 特征—物品相关推荐
    • 过滤模块
    • 排名模块
• 评分预测问题
  • 评分预测算法
    • 平均值
      • 用户分类对物品分类的平均值
      • 基于邻域的方法
      • 隐语义模型与矩阵分解模型
      • 加入时间信息
      • 模型融合

推荐系统实例

外围架构

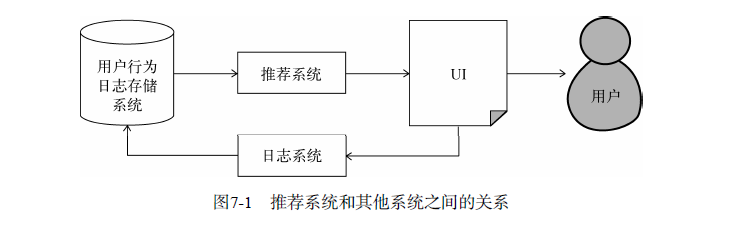
一般来说，需要实时存取的数据存储在数据库和缓存中，而大规模的非实时地存取数据存储在分布式
文件系统（如HDFS）中。数据能否实时存取在推荐系统中非常重要，因为推荐系统的实时性主要依赖于能否实时拿到用户的新行为。只有快速拿到大量用户的新行为，推荐系统才能够实时地适应用户当前的需求，
给用户进行实时推荐。

推荐系统架构

推荐系统需要由多个推荐引擎组成，每个推荐引擎负责一类特征和一种任务，而推荐系统的任务只是将推荐引擎的结果按照一定权重或者优先级合并、排序然后返回。

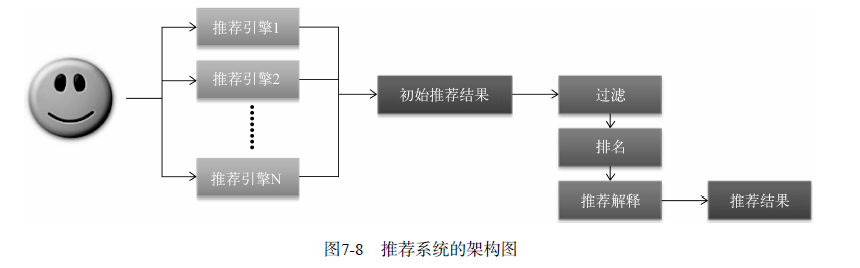
好处：

• 可以方便地增加/删除引擎，控制不同引擎对推荐结果的影响。
• 可以实现推荐引擎级别的用户反馈。

推荐引擎的架构

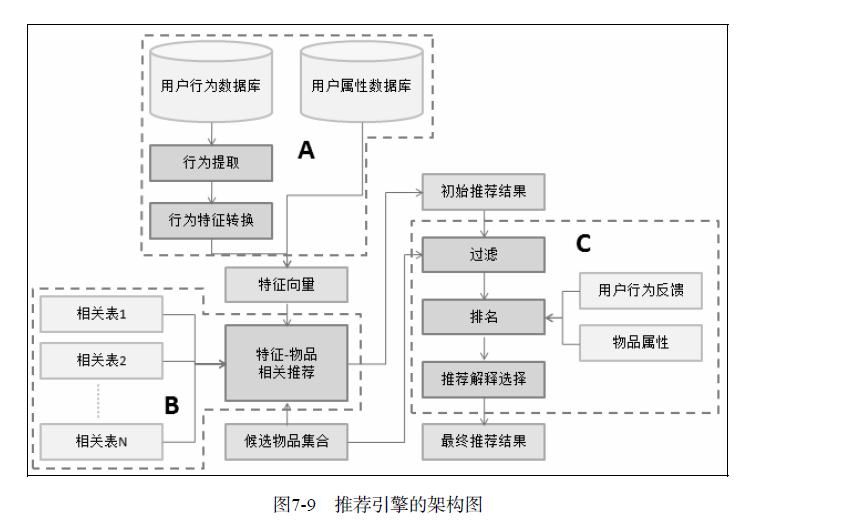
• A负责从数据库或者缓存中拿到用户行为数据，通过分析不同行为，生成当前用户的特征向量。不过如果是使用非行为特征，就不需要使用行为提取和分析模块了。该模块的输出是用户特征向量。
• B负责将用户的特征向量通过特征-物品相关矩阵转化为初始推荐物品列表。
• C负责对初始的推荐列表进行过滤、排名等处理，从而生成最终的推荐结果。

生成用户特征向量

用户的特征包括两种，一种是用户的注册信息中可以提取出来的，另一种特征主要是从用户的行为中计算出来的。
一个特征向量由特征以及特征的权重组成，在利用用户行为计算特征向量时需要考虑以下因素。

• 用户行为的种类
• 用户行为产生的时间
• 用户行为的次数
• 物品的热门程度

特征—物品相关推荐

在得到用户的特征向量后，可以根据离线的相关表得到初始的物品推荐列表，存储和它最相关的N个物品的ID。特征—物品相关推荐模块还可以接受一个候选物品集合。候选物品集合的目的是保证推荐结果只包含候选物品集合中的物品。
什么不在过滤模块中过滤掉不在候选集中的物品：防止错失推荐低热度的物品。（候选物品集合较小的情况下）

过滤模块

在得到初步的推荐列表后，还不能把这个列表展现给用户，首先需要按照产品需求对结果进
行过滤，过滤掉那些不符合要求的物品。

• 用户已经产生过行为物品
• 候选物品以外的物品
• 某些质量很差的物品

排名模块

1. 新颖性排名
   
2. 多样性
   第一种提高多样性的方法是将推荐结果按照某种物品的内容属性分成几类，然后在每个类中
   都选择该类中排名最高的物品组合成最终的推荐列表。第二种提高推荐结果多样性的方法是控制不同推荐结果的推荐理由出现的次数。
3. 时间多样性
   时间多样性主要是为了保证用户不要每天来推荐系统都看到同样的推荐结果。

• 记录用户每次登陆推荐系统看到的推荐结果。
• 将这些结果发回日志系统。这种数据不需要实时存储，只要能保证小于一天的延时就足
  够了。
• 在用户登录时拿到用户昨天及之前看过的推荐结果列表，从当前推荐结果中将用户已经
  看到的推荐结果降权。

4. 用户反馈
   排名模块最重要的部分就是用户反馈模块。用户反馈模块主要通过分析用户之前和推荐结果
   的交互日志，预测用户会对什么样的推荐结果比较感兴趣。
   如果推荐系统的目标是提高用户对推荐结果的点击率，那么可以利用点击模型（click model）
   预测用户是否会点击推荐结果。点击率预测中可以用如下特征预测用户u会不会点击物品i：

• 用户u相关的特征，比如年龄、性别、活跃程度、之前有没有点击行为；
• 物品i相关的特征，比如流行度，平均分，内容属性；
• 物品i在推荐列表中的位置。用户的点击和用户界面的设计有很高的相关性，因此物品i在
  推荐列表中的位置对预测用户是否点击很重要；
• 用户之前是否点击过和推荐物品i具有同样推荐解释的其他推荐结果；
• 用户之前是否点击过和推荐物品i来自同样推荐引擎的其他推荐结果。

评分预测问题

评分预测算法

平均值

最简单的评分预测算法是利用平均值预测用户对物品的评分的。

用户分类对物品分类的平均值

基于邻域的方法

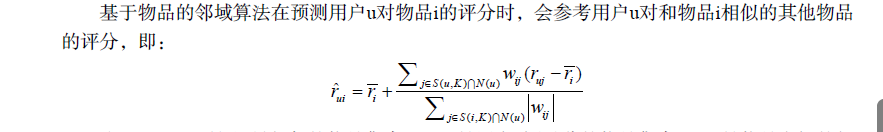
隐语义模型与矩阵分解模型

用户的评分行为可以表示成一个评分矩阵R，其中R[u][i]就是用户u对物品i的评分。但是，用户不会对所有的物品评分，所以这个矩阵里有很多元素都是空的，评分预测从某种意义上说就是填空。
1.传统的SVD分解
给定m个用户和n个物品，和用户对物品$R\inℝ^{m \times n}$。首先需要对评分矩阵中的缺失值进行简单地补全，比如用全局平均值，或者用户/物品平均值补全，得到补全后的矩阵R'。接着，可以用SVD分解将R'分解成如下形式：

$R'=U^TSV$

其中$U \inℝ^{k \times m}$，$V \inℝ^{k \times n}$是两个正交矩阵，$S \inℝ^{k \times k}$是对角阵，对角线上的每一个元素都是矩阵的奇异值。为了对R'进行降维，可以取最大的$f$个奇异值组成对角矩阵$S_f$，并且找到这$f$个奇异值中每个值在U、V矩阵中对应的行和列，得到$U_f$、$V_f$，从而可以得到一个降维后的评分矩阵：

$R_f'=U_f^TS_fV_f$

其中， $R_f'(u,i)$ 就是用户u对物品i评分的预测值。
缺点：

• 补全后变稠密矩阵，消耗内存空间。
• 计算复杂度很高

2. Simon Funk的SVD分解
   
3. 加入偏置项后的LFM
   
   
4. 考虑邻域影响的LFM
   前面的LFM模型中并没有显式地考虑用户的历史行为对用户评分预测的影响，提出SVD++。
   

加入时间信息

1. 基于邻域的模型融合时间信息
   
2. 基于矩阵分解的模型融合时间信息
   在引入时间信息后，用户评分矩阵不再是一个二维矩阵，而是变成了一个三维矩阵。我们可以仿照分解二维矩阵的方式对三维矩阵进行分解。
   

模型融合

1. 模型级联融合
2. 模型加权融合